8ºA, 8ºB, 8ºC e 8ºD
Matemática
Professora Simone e professor Ricardo
Boa tarde!
Espero que estejam bem.
Estamos com saudades.
1- Segue a correção das atividades 1.1, 1.2, 1.3, 1.6 e 1.7,do caderno do aluno, volume 2,parte 1, páginas 68, 69 e 70.
2- Seguem alguns exercícios para realizarem até o dia 17/7/2020.
Bom final de semana.
Correção
1.1
a) P=
perímetro e l = lado
P
= 4· l
Exemplo: Se l = 1 cm
P = 4 · 1 = 4 cm
Se l = 2 cm P = 4 · 2
= 8 cm
Assim, se a medida do lado dobrar, a medida do perímetro
também dobra. Quando aumenta o lado do quadrado, seu perímetro aumenta na mesma
proporção. São grandezas diretamente proporcionais.
b) Se a velocidade média dobrar, o tempo que um automóvel
levará para percorrer uma certa distância cairá pela metade.Quanto maior a
velocidade média, o tempo de percurso será proporcionalmente menor. São
grandezas inversamente proporcionais.
c) Se todos os
funcionários tem o mesmo ritmo de trabalho, se dobrarmos a quantidade de
funcionários de uma fábrica, o número de produtos fabricados dobrará. Quanto
mais funcionários, a produtividade é proporcionalmente maior, considerando que
todos trabalhem no mesmo ritmo. São
grandezas diretamente proporcionais.
d) Se dobrarmos a
distância percorrida por um veículo, a quantidade de combustível usado dobrará.
Quanto maior à distância, o consumo de combustível será proporcionalmente maior.
São grandezas diretamente proporcionais.
e) Se todos os trabalhadores tem o mesmo ritmo de trabalho,
se dobrarmos a quantidade de trabalhadores, a construção do muro dobrará. Quanto
maior a quantidade de trabalhadores, a quantidade de muro construído será proporcionalmente maior, sendo
mantido o mesmo ritmo de trabalho. São grandezas diretamente proporcionais.
1.2
São inversamente proporcionais. Ao dobrarmos a
velocidade, o tempo é reduzido pela metade.
1.3
a) Porque ao dobrar a quantidade de produtos, o
valor a ser pago também dobra.
b) P = 70 n, onde P
representa o valor pago e n representa a quantidade de produtos.
c) P = 70 n
P = 70 x 18
P = 1 260
Logo, caso essa pessoa compre as 18 unidades, ela irá pagar
R$ 1 260,00.
d) P = 70 n P =
3360
360 = 70 n
3360 : 70 = n
48 = n
Logo, a quantidade de
produtos comprados com R$ 3 360,00 é de 48 unidades.
e) Substituindo o
valor de n por 1, temos:
P = 70n
P = 70 x 1
P = 70
Um produto custará R$
70,00.
1.6 a) C · x
= 36 , sendo C o comprimento e x a largura.
b) . Inversamente
proporcionais. Se dobrar a medida da largura, a medida do comprimento cairá
pela metade, para manter a área do retângulo.
1.7 a) 1 kg de tomates= R$ 1,50
2 kg de tomates = 2 x 1,50 = R$ 3,00
b) 1 kg de tomates= R$ 1,50
5 kg de tomates = 5 x 1,50 = R$ 7,50
c) 1 kg de tomates= R$ 1,50
7 kg de tomates = 7 x 1,50 = R$ 10,50
d) São grandezas diretamente
proporcionais. Se dobrar os quilos de tomates, dobrará o preço.
Exercícios
1- Calcule a área de um retângulo cujo comprimento é 45 metros e a largura é 38 metros.
2- Qual é o
comprimento de um retângulo cuja largura mede 118 metros e a área total é de
472 m2 ?
.
3- Calcule
a área da figura abaixo:
10 cm
12cm 12 cm
12 cm
5cm
 12 cm
12 cm5cm
a)
|
b)
|
d)
|
Segue os links da aulas do centro de mídias:
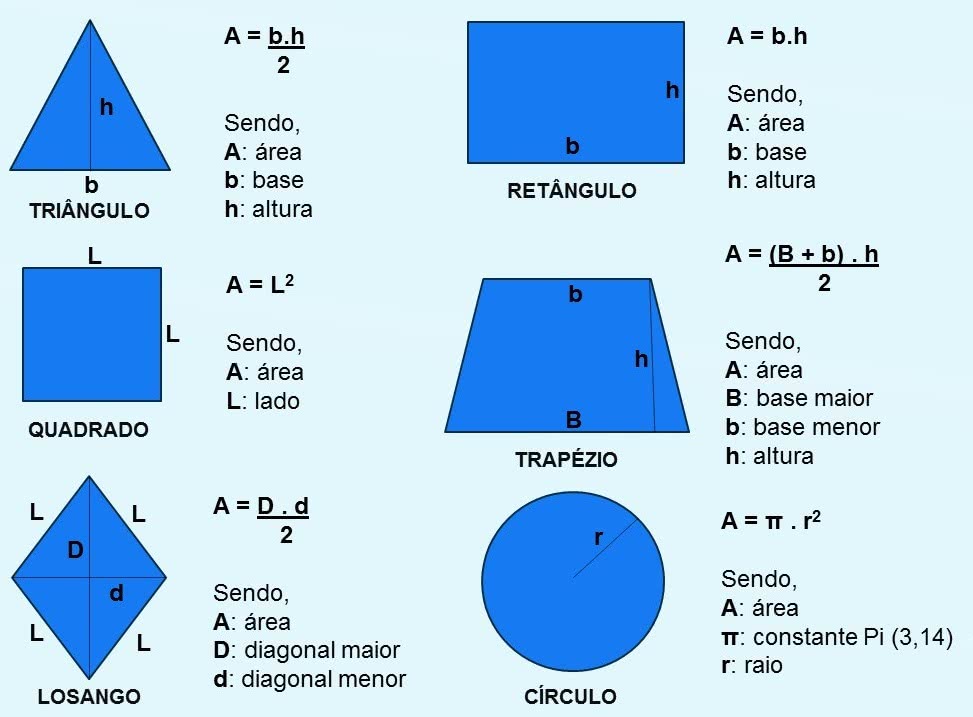
Fórmula das Áreas das Figuras Planas
Confira abaixo as fórmulas para os cálculos de área:


Nenhum comentário:
Postar um comentário